Handling speckle noise on SAR images

Local methods

The design of efficient despeckling filters is a long-standing problem that has been the object of intense research since the advent of SAR technology. The most straightforward way to reduce these fluctuations and estimate the values of the physical parameters is to average several independent samples from the data. This operation, called multilooking, was applied in various forms from the very beginning of the SAR era. However, such averaging that applies equally to every region of the image, regardless of the local heterogeneity, strongly degrades the spatial resolution.

In the beginning of 2000s, Lee et al. proposed to use adaptive filtering for polarimetric and interferometric SAR denoising. Instead of estimating the parameters over a rectangular sliding window, a directional window is locally selected among eight edge-aligned windows according to the local gradient of the amplitude images. Lee’s method preserves the edge structures since values of pixels on each side of the edge are never combined together, avoiding the smoothing effects. Unfortunately, this method tends to leave a high variance in homogeneous areas and create some undesired artifacts.

The intensity-driven adaptive-neighborhood (IDAN) technique was proposed for the polarimetric and interferometric SAR parameter estimation. Following the idea of filtering over directional windows, the IDAN performs a complex multilooking operation on an adaptive neighborhood. This adaptive neighborhood is constructed with a region-growing algorithm where the most similar adjacent pixels are selected iteratively according to their intensity values. The adaptive neighborhood aims to select as many pixels as possible, all following the same statistical population as the considered pixel. This decreases the resolution loss in the estimation since noisy values coming from other populations are rejected. Due to its window-shaped adaptivity, the IDAN achieves the best trade-off between the residual noise and resolution loss among window-based methods. However, due to its connectivity constraint, the IDAN leaves a high variance in regions where there are only few adjacent similar pixels.

The following generation of filtering approaches introduced stronger priors to guide the solution. The first family includes the variational-based methods which have gradually been utilized for SAR image despeckling. Those methods are stable and flexible and break through the traditional idea of filters by solving the problem of energy optimization. Although these methods have achieved good reduction of speckle noise, the result is usually dependent on the choice of the model parameters and prior information, and is often time-consuming. In addition, the variational-based methods cannot accurately describe the distribution of speckle noise, which also constraints the performance of speckle noise reduction.

The second large family of approaches is based on wavelet transforms. Due to their spatially localized and multiresolution basis functions, wavelets yield sparse yet accurate representations of natural images in the transform domain. Sharp discontinuities and pointlike features, so common in SAR images, are well described by a small number of basis functions, just like the large homogeneous regions between them. The major weaknesses of this type of approach are the backscatter mean preservation in homogeneous areas, details preservation, and producing artificial effect into the results such as ring effects.

Non-local methods

The non-local means (NLM) algorithm has provided a breakthrough in detail preservation in SAR image despeckling. During the recent years, powerful and widespread methods such as PPB, NL-SAR and SAR-BM3D have been created. In the following paragraph, we will describe the essentials of the algorithm. Figure 1 summarizes the processing steps. 

Figure 1. Non-local estimation in action: processing at pixel x.

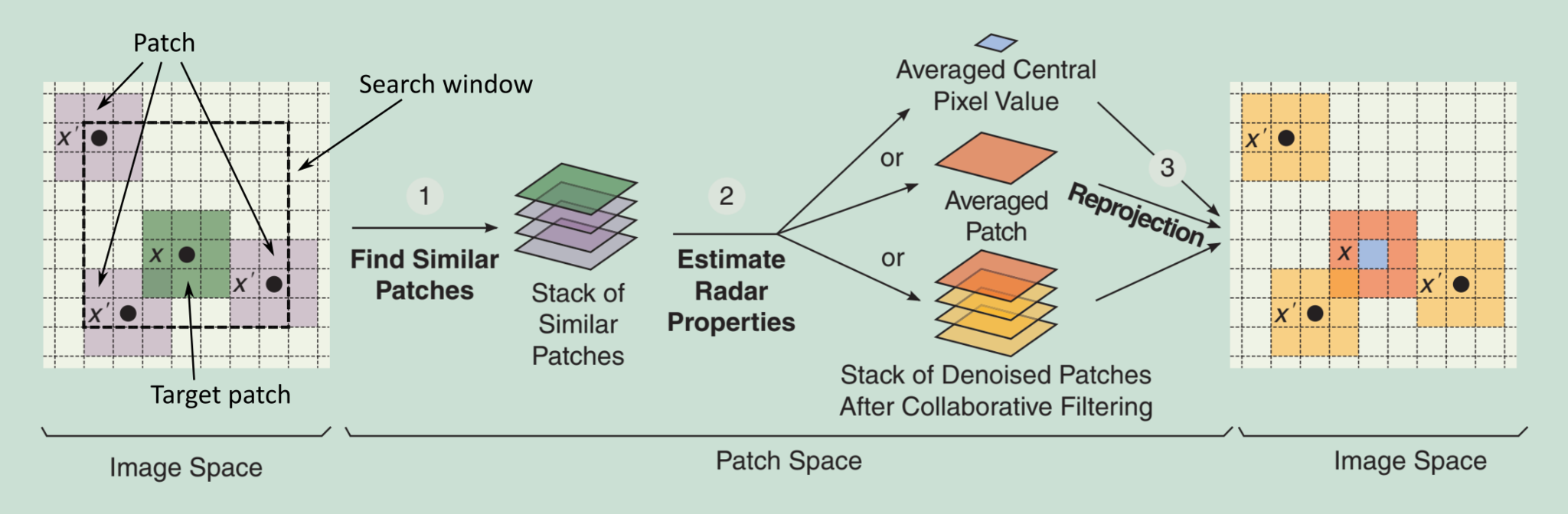
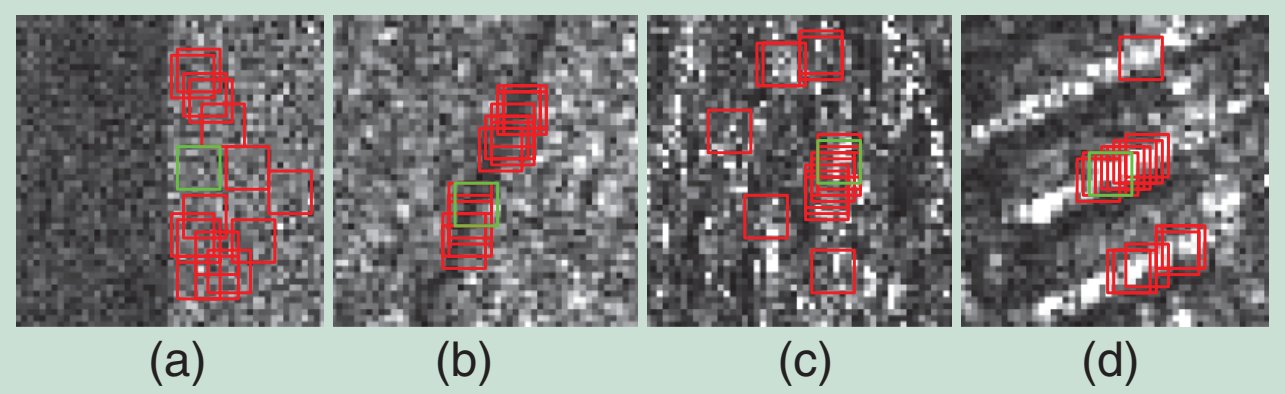
Non-local estimation methods generally follow a three-step scheme with many possible variations at each step and, possibly, preprocessing steps and/or iterative refinement of results by repeated non-local estimations. The first step identifies similar patches (patch size is generally set from 3x3 to 11x11 pixels). It must reliably find, within an extended search window (typically 21x21 to 39x39 pixels), patches that are close to the reference central patch. Recurring patches are found in smooth regions, but just as well around region boundaries, textures, artificial structures, etc., as shown in figure 2. Once several patches have been selected, they are assigned relative weights.

Figure 2. Fragments of SAR images: (a) homogeneous region, (b) line, (c) texture, (d) structure. For each target patch (green) several similar patches (red) are found in the same fragment [1].

The second step combines patches, according to their weights, to form an estimate of either the central pixel (pixel-wise estimation), the central patch (patch-wise estimation), or all selected patches (stack-wise estimation). The estimates computed from all possible reference patches are then merged in a last step to produce the final image.

The most straightforward way to combine patches is to use pixel-wise filtering. Within this approach, a weight is assigned for the central pixel of all the patches. By using those weights, the estimation for the central pixel in a target patch is calculated.

The difference in patch-wise filtering is that all pixels in the patch, not just the central one, are estimated at once. Since each pixel is estimated several times, a suitable aggregation phase is necessary to combine all such estimates. The simplest form of aggregation is to consider uniform weights for all the estimated pixels. Another strategy is to set the weight associated with each estimate as inversely proportional to its variance.

To illustrate why patch-wise estimation improves performance, let us consider the special case of a pixel near the boundary between two homogeneous regions. Since the patch centered on it is strongly heterogeneous, most other patches of the search area, coming from homogeneous regions on either side of the boundary, are markedly dissimilar from it, and contribute very little to the average. The estimate, thus, involves only a small effective number of predictors, those along the edge, which results in a high variance. As a result, a visible “halo” of residual noise is observed near the edges, a phenomenon well-known in NLM, also referred to as the rare patch effect. The target pixel, however, belongs to a large number of patches, not just the patch centered on it, many of them drawn from the homogeneous region to which the pixel belongs. In patch-wise reprojection, all of these patches are included in the average reducing the estimate variance, especially if suitable weights are used to take into account the reliability of each contribution.

Let us now consider the third strategy, with stack-wise filtering. The first difference with regard to patch-wise filtering is that now all patches collected in the stack are collaboratively filtered before reprojecting them to their original position. The major improvement is that the stack is filtered in three dimensions, i.e, not only along the stack but also in the spatial domain. In SAR-BM3D, the whole stack, formed by just a limited number of similar patches, is wavelet transformed, Wiener filtered, and back transformed. By so doing, strong spatial structures are emphasized through filtering while random noise is efficiently suppressed. As a matter of fact, these techniques exhibit significant improvements especially in highly structured areas (edges, point reflectors, textures). The efficiency of collaborative filtering comes from the full exploitation of the redundancy of information in a stack of similar patches.

The performance of NLM methods depends on the setting of several parameters, like patch size and search area size, which should be related to image resolution, smoothing strength, and balance between original and pre-estimated data. In most of the non-local approaches these parameters are set by hand. Few works have considered semisupervised setting or automatic setting with spatial adaptation. NL-SAR is one of such publicly available methods that automatically tunes patch and search window sizes and prefiltering strengths to provide improved results.

Speckle filtering in KappaZeta

In KappaZeta we analyzed, modified and combined multiple published methods when designing a custom speckle filter for KappaOne service. For details, take a look at our newsletter from April 2022.